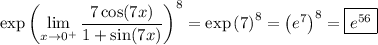Question

Lim x-> 0^+ (1+sin7x)^8/x

Answer 1

If you mean

`\displaystyle \lim_(x\to0^+) \frac{(1+\sin(7x))^8}x`

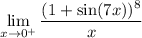
then the limit doesn't exist, since 1 + sin(7x) approaches 1 while the denominator approaches 0.

However, if instead you mean

`\displaystyle \lim_(x\to0^+)(1+\sin(7x))^(8/x)`

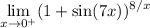
rewrite the limand as

`(1+\sin(7x))^(8/x) = \exp\left(\ln(1+\sin(7x))^(8/x)\right) \\\\ = \exp\left(\frac{8\ln(1+\sin(7x))}x\right) \\\\ =\exp\left(\frac{\ln(1+\sin(7x))}x\right)^8`

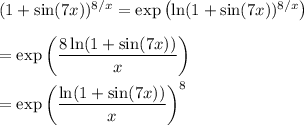
The exponential function is continuous at 0, so we can pass the limit through it:

`\displaystyle\lim_(x\to0^+)\exp\left(\frac{\ln(1+\sin(7x))}x\right)^8 = \exp\left(\lim_(x\to0^+)\frac{\ln(1+\sin(7x))}x\right)^8`

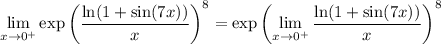
The remaining limit takes the indeterminate form 0/0, since ln(1 + sin(7x)) approaches ln(1) = 0, and so does x in the denominator. Apply L'Hopital's rule:

`\displaystyle\exp\left(\lim_(x\to0^+)(7\cos(7x))/(1+\sin(7x))\right)^8 = \exp\left(7\right)^8 = \left(e^7\right)^8 = \boxed{e^(56)}`