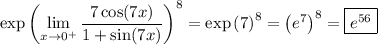If you mean
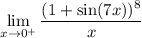
then the limit doesn't exist, since 1 + sin(7x) approaches 1 while the denominator approaches 0.
However, if instead you mean
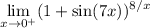
rewrite the limand as
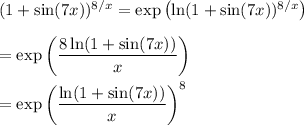
The exponential function is continuous at 0, so we can pass the limit through it:
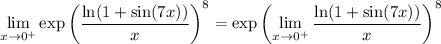
The remaining limit takes the indeterminate form 0/0, since ln(1 + sin(7x)) approaches ln(1) = 0, and so does x in the denominator. Apply L'Hopital's rule: