Answer:

Explanation:
The formula for calculating the distance between 2 points is:
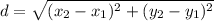
In this formula, (x₁, y₁) and (x₂, y₂) are the 2 points. The 2 points we are given are (-4, 6) and (3, -7). If we match the value with the corresponding variable we see that:
- x₁ = -4
- y₁ = 6
- x₂ = 3
- y₂ = -7
Substitute the values into the formula.
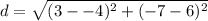
Solve inside the parentheses.
- (3--4) = (3+4) = 7
- (-7-6) = -13
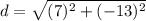
Solve the exponents.
- (7)²= 7*7 = 49
- (-13)² = -13 * -13 = 169
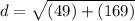
Add.
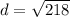
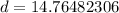
If we round to the nearest hundredth place, the 4 in the thousandth place tells us to leave the 6.
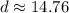
The distance between the points (-4, 6) and (3, -7) is √218 or approximately 14.76.