Question

How do i find the slope

Answer 1

Hi, I'm happy to help!

To find the slope, you need to use the slope formula, where m is the slope:

m=
`(y_(2)-y_(1 ) )/(x_(2) -x_(1) )`

Slope means rise over run, or how much the line rises per the amount the line moves forward. This equation shows the movement from the y points to show rise, over the difference in the x points to show run.

Now, to find the slope we insert our values, starting with our second y point:

m=
`(2-y_(1 ) )/(x_(2) -x_(1) )`

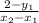
Now insert our first y point:

m=
`(2-4 )/(x_(2) -x_(1) )`

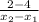
Now we insert our second x point:

m=
`(2-4 )/(-3 -x_(1) )`

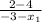
And finally our first x point:

m=
`(2-4 )/(-3 -3 )`

Now, we solve:

m=
`(-2 )/(-6)`

So, our slope is -2/-6, to simplify it, we remove both negatives because they cancel each other out.

m=
`(2 )/(6)`

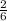
Now, we simplify our fraction by dividing the top and bottom by 2:

m=
`(1)/(3)`

So, our slope is 1/3. This means that for every 1 unit the line rises, it goes to the right 3 units. The y-intercept is where the line hits the y axis.

If the question is asking for slope intercept form for the equation, you use y=mx+b

y represents any y coordinate on your line, m represents your slope (1/3), x represents any x coordinate on your line, and b represents your y-intercept (3).

If you were to insert these values, you would get:

y=
`(1)/(3)`x+3

You use this to find what a y coordinate would be so you can draw your line.

For the next equation we do the same thing:

m=
`(y_(2)-y_(1 ) )/(x_(2) -x_(1) )`

Insert our values:

m=
`(4-1)/(2-(-4))`

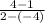
Get rid of the double negative:

m=
`(4-1)/(2+4)`

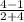
Solve:

m=
`(3)/(6)`

Simplify:

m=
`(1)/(2)`

Now that we know our slope, let's plug it in to our slope intercept form equation.

y=
`(1)/(2)`x+3

I hope this was helpful! Keep learning! :D