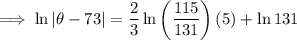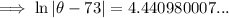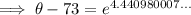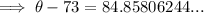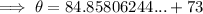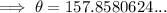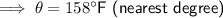Answer:
158°F (nearest degree)
Explanation:
Solving using Newton's Law of Cooling
Newton's Law of Cooling Formula:
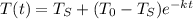
where:
-
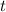 = time
= time -
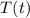 = temperature of the water at time (t)
= temperature of the water at time (t) -
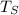 = surrounding temperature
= surrounding temperature -
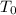 = initial temperature of the water
= initial temperature of the water -
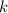 = constant
= constant
Given:
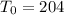
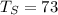
- T(t) = 188 when t = 1.5m
Substituting given values into the formula and solve for k:
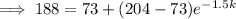
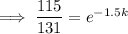
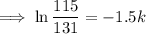
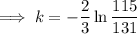
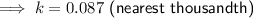
So the final equation is:
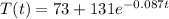
Therefore, when t = 5:
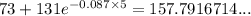
= 158 °F (nearest degree)
Solving using differential equations
The temperature (
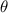 ) of the cup of water will decrease proportionally to the difference between the temperature of the water (
) of the cup of water will decrease proportionally to the difference between the temperature of the water (
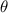 ) and the temperature of the room (73°F):
) and the temperature of the room (73°F):
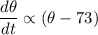
Change this to an equation by introducing a constant k. As the rate of change of temperature is decreasing, we need to introduce a negative sign:
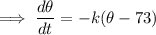
Now solve the differential equation:
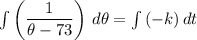
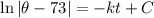
To find the constants k and C, use the given conditions:
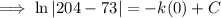
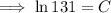
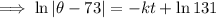
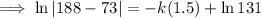

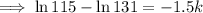
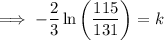
Therefore, final equation:
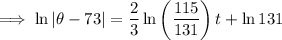
When t = 5: