Question

Simplify.
6i/9+2i

A. 81-18i/85
B. 2i/3
C. 6i/13
D. 12+54i/85

Answer 1

D

Explanation:

We want to simplify the expression:

`\displaystyle (6i)/(9+2i)`

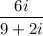
To do so, we can remove the imaginary unit in the denominator by multiply it by the conjugate.

The conjugate of a + bi is a - bi.

Hence, we will multiply the fraction by 9 - 2i:

`\displaystyle =(6i)/(9+2i)\left((9-2i)/(9-2i)\right)`

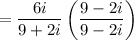
Multiply:

`\displaystyle = (6i(9-2i))/((9+2i)(9-2i))`

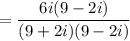
Difference of two squares:

`\displaystyle = (6i(9-2i))/((9)^2 -(2i)^2)`

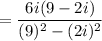
Simplify:

`\displaystyle = (54i-12i^2)/((81)-(4i^2)) = (54i-(-12))/(81-(-4)) = (12+54i)/(85)`

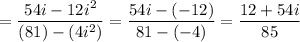
Hence, our answer is D.