The simplified form of
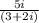 is
is
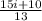 . Option A is the right choice.
. Option A is the right choice.
To simplify
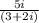 , we can multiply both the numerator and denominator by the conjugate of the denominator, which is 3−2i.
, we can multiply both the numerator and denominator by the conjugate of the denominator, which is 3−2i.
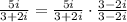
Using the distributive property and the fact that
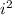 =−1, we can simplify the denominator as follows:
=−1, we can simplify the denominator as follows:

Substituting
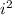 =−1, we get:
=−1, we get:

Option A is the right choice.