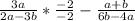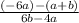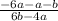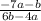Answer:
C)
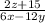
E)
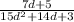
F)
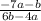
Explanation:
C)
One is given the following equation
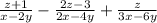
In order to simplify fractions, one must convert the fractions to a common denominator. The common denominator is the least common multiple between the given denominators. Please note that the denominator is the number under the fraction bar of a fraction. In this case, the least common multiple of the denominators is (
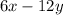 ). Multiply the numerator and denominator of each fraction by the respective value in order to convert the fraction's denominator to the least common multiple,
). Multiply the numerator and denominator of each fraction by the respective value in order to convert the fraction's denominator to the least common multiple,
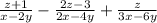
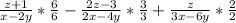
Simplify,
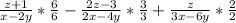
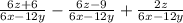

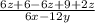
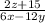
E)
In this case, one is given the problem that is as follows:
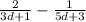
Use a similar strategy to solve this problem as used in part (c). Please note that in this case, the least common multiple of the two denominators is the product of the two denominators. In other words, the following value: (
 )
)
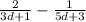
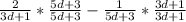
Simplify,
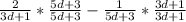


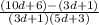

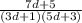
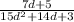
F)
The final problem one is given is the following:

For this problem, one can use the same strategy to solve it as used in parts (c) and (e). The least common multiple of the two denominators is (
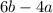 ). Multiply the first fraction by a certain value to attain this denomaintor,
). Multiply the first fraction by a certain value to attain this denomaintor,

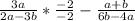
Simplify,