Question

Help meeee asap how to do this

Answer 1

Answer:
`(3)/(4)(2+t)^(4/3)+C\\\\`

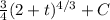
where C is a constant.

=========================================================

Step-by-step explanation:

Apply u-substitution

`u = 2+t\\\\(du)/(dt) = 1\\\\du = dt`

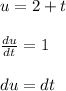
So,

`\displaystyle \int \sqrt[3]{2+t}\ \ dt = \int (2+t)^(1/3)\ dt\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = \int (u)^(1/3) \ du\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = (1)/(1+1/3)(u)^(1+1/3)+C\\\\`

`\displaystyle \int \sqrt[3]{2+t}\ \ dt = (1)/(4/3)(u)^(4/3)+C\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = (3)/(4)(u)^(4/3)+C\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = (3)/(4)(2+t)^(4/3)+C\\\\`

Don't forget about the plus C at the end.

---------------------------

The rule used in step 3 is

`\displaystyle \int x^n \ dx = (1)/(n+1)x^(n+1)+C`

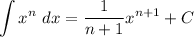
To verify the answer, apply the derivative to both sides and you should find that

`\displaystyle (d)/(dt)\int \sqrt[3]{2+t}\ \ dt = (d)/(dt)\left[(3)/(4)(2+t)^(4/3)+C\right] = \sqrt[3]{2+t}\\\\`

I'm skipping a bit of steps.

This is an example of the fundamental theorem of calculus to tie together the inverse operations of derivatives vs integrals (aka antiderivatives).

WolframAlpha is a tool you can use to verify the answer.