Answer:
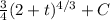
where C is a constant.
=========================================================
Step-by-step explanation:
Apply u-substitution
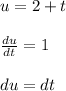
So,
![\displaystyle \int \sqrt[3]{2+t}\ \ dt = \int (2+t)^(1/3)\ dt\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = \int (u)^(1/3) \ du\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = (1)/(1+1/3)(u)^(1+1/3)+C\\\\](https://img.qammunity.org/2023/formulas/mathematics/college/9872ocukhbm0i6fw6efmzi1ibwtctjecpy.png)
![\displaystyle \int \sqrt[3]{2+t}\ \ dt = (1)/(4/3)(u)^(4/3)+C\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = (3)/(4)(u)^(4/3)+C\\\\\displaystyle \int \sqrt[3]{2+t}\ \ dt = (3)/(4)(2+t)^(4/3)+C\\\\](https://img.qammunity.org/2023/formulas/mathematics/college/yzkckx17y7j3cfr55o60q0uecw1mhtfv0g.png)
Don't forget about the plus C at the end.
---------------------------
The rule used in step 3 is
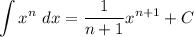
To verify the answer, apply the derivative to both sides and you should find that
![\displaystyle (d)/(dt)\int \sqrt[3]{2+t}\ \ dt = (d)/(dt)\left[(3)/(4)(2+t)^(4/3)+C\right] = \sqrt[3]{2+t}\\\\](https://img.qammunity.org/2023/formulas/mathematics/college/xliao807032k8ahls8w4mwjecvwb7w86b8.png)
I'm skipping a bit of steps.
This is an example of the fundamental theorem of calculus to tie together the inverse operations of derivatives vs integrals (aka antiderivatives).
WolframAlpha is a tool you can use to verify the answer.