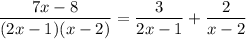We look for constants a and b such that

Rewrite all terms with a common denominator and set the numerators equal:
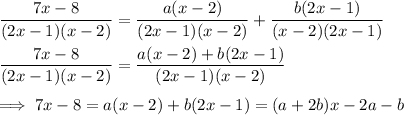
Then
a + 2b = 7
-2a - b = -8
Solve for a and b. Using elimination: multiply the first equation by 2 and add it to the second equation:
2 (a + 2b) + (-2a - b) = 2(7) + (-8)
2a + 4b - 2a - b = 14 - 8
3b = 6
b = 2
Then
a + 2(2) = 7 ==> a = 3
and so