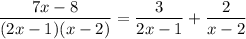Question

Given that (7x-8)/(2x-1)(x-2)

Use Partial Fraction Decomposition to Find A and B.

Answer 1

a=3

b=2

Do whatever you want with that information^^

Answer 2

We look for constants a and b such that

`\displaystyle (7x-8)/((2x-1)(x-2)) = \frac a{2x-1} + \frac b{x-2}`

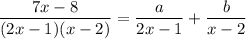
Rewrite all terms with a common denominator and set the numerators equal:

`\displaystyle (7x-8)/((2x-1)(x-2)) = (a(x-2))/((2x-1)(x-2)) + (b(2x-1))/((x-2)(2x-1)) \\\\ (7x-8)/((2x-1)(x-2)) = (a(x-2)+b(2x-1))/((2x-1)(x-2)) \\\\ \implies 7x-8 = a(x-2) + b(2x-1) = (a+2b)x - 2a - b`

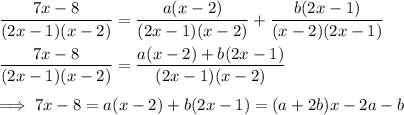
Then

a + 2b = 7

-2a - b = -8

Solve for a and b. Using elimination: multiply the first equation by 2 and add it to the second equation:

2 (a + 2b) + (-2a - b) = 2(7) + (-8)

2a + 4b - 2a - b = 14 - 8

3b = 6

b = 2

Then

a + 2(2) = 7 ==> a = 3

and so

`\displaystyle (7x-8)/((2x-1)(x-2)) = \frac 3{2x-1} + \frac 2{x-2}`