Question

A product is introduced into the market. Suppose a products sales quantity per month q(t) is a function of time t in months is given by q(t) = 5000t-120t^2. And suppose the price in dollars of that product. p(t). is also a function of time t in months and is given by p(t) = 120-t^2.

Required:
a. Find, R'(t). the rate of change of revenue as a function of time t
b. What is the the rate of change of revenue with respect to time 3 months after the introduction?

Answer 1

Part A)

`\displaystyle R'(t) = (5000-240t)(120-t^2)+(5000t-120t^2)(-2t)`

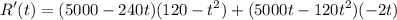
Part B)

After three months, the revenue is increasing at a rate of $391,560 per month.

Explanation:

A product is introduced into the market. The quantity per month q sold is given by the function:

`q(t) = 5000t - 120t^2`

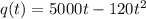
And the price p (in dollars) of the product is given by the function:

`p(t) = 120-t^2`

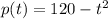
Part A)

R(t), or the revenue, will be the product of the quantity sold and its respective price during the month. Hence:

`\displaystyle R(t) = q(t)\cdot p(t)`

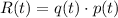
Substitute:

`\displaystyle R(t) = \left(5000t-120t^2\right)\left(120-t^2\right)`

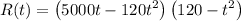
To find R'(t), take the derivative of both sides with respect to t:

`\displaystyle R'(t) = (d)/(dt)\left[ \left(5000t-120t^2\right)\left(120-t^2\right)\right]`

Since the function is a product of two expressions, we can consider using the Product Rule:

`\displaystyle (d)/(dx) \left[uv\right] = u'v+uv'`

Hence:

`\displaystyle R'(t) = (d)/(dt)\left[5000t-120t^2\right]\left(120-t^2\right) + \left(5000t-120t^2\right)(d)/(dt)\left[120-t^2\right]`

Differentiate. Therefore:

`\displaystyle R'(t) = (5000-240t)(120-t^2)+(5000t-120t^2)(-2t)`

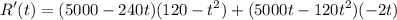
(We may simplify if we desire, but this is not required by the problem.)

Part B)

To find the rate of change of revenue with respect to time three months after the introduction, we can evaluate R'(t) at t = 3. Hence:

`\displaystyle R'(3) = (5000-240(3))(120-(3)^2)+(5000(3)-120(3)^2)(-2(3))`

Evaluate:

`R'(3) = 391560\text{ dollars/month}`

In conclusion, after three months, the revenue is increasing at a rate of $391,560 per month.

(Note: it is increasing because the final value is positive.)