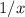Question

Help solve pls fast
it's a maths question ​

Answer 1

`1/x`

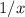
Explanation:

To simplify, work from the inside out.

We start with

`\sqrt[4]{x^(3/4)}`

on the inside. And we can change the fourth root into a fractional exponent -- 1/4:

`(x^{(3)/(4))^(1/4)`

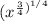
A power of a power means multiply the exponents, giving

`x^{(3)/(4) * (1)/(4)} = x^(3/16)`

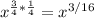
So now we have

`[(x^(3/16))^(-4/3)]^4`

From here, apply the "power of a power rule" again, working from the inside out.

`(x^(-12/48))^4`

`x^(-48/48)`

`x^(-1)`

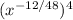
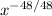
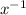
or

`1/x`

Answer 2

Explanation:

`[(\sqrt[4]{x^{(3)/(4)}})^{(-4)/(3)} ]^(4)`

`= [(x^{(3)/(4)*(1)/(4)})^{(-4)/(3)}]^(4)\\\\\\= [(x^{(3)/(16) ) ^{(-4)/(3)}}]^(4)\\\\=[ x^{(3)/(16)*(-4)/(3)}]^(4)\\\\=[x^{(-1)/(4)}]^(4)\\\\=x^{(-1)/(4)*4}\\\\=x^(-1)\\\\=(1)/(x)`

Hint:

`(a^(m))^(n)=a^(m*n)`