Help me please I need help to my question √(50) + \sqrt[]{18} - 8 \sqrt[]{2}

Question

asked Mar 28, 2022 157k views

2 Answers

Willi · Answer 1 · 2022-04-03T12:32:24+0000

Given the expression:

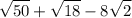
$\displaystyle \large{ √(50) + √(18) - 8 √(2) }$

Since we have 2 in the square root from 8√2. We will be converting terms in √2 form so we can. evaluate.

As we know, 50 comes from 5×10 = 5×5×2

and 18 comes from 9×2 = 3×3×2.

$\displaystyle \large{ √(5 * 5 * 2) + √(3 * 3 * 2) - 8 √(2) }$

In the square root, if there are two same numbers, we can pull it out as one.

Ex. √5×5 would be 5. Refer to below:

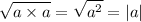
$\displaystyle \large{ √(a * a) = \sqrt{ {a}^(2) } = |a| }$

Since there are two fives and two threes in the square root, we pull these numbers out only one.

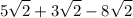
$\displaystyle \large{ 5√(2) + 3 √(2) - 8 √(2) }$

Because these terms have the same square root of 2, we can evaluate 5+3-8.

$\displaystyle \large{ 8 √(2) - 8 √(2) } = 0$

Of course, like term - like term = 0

Hence, the answer is 0.