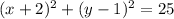Question

Write the equation of circle with diameter of 10 units centered at (- 2, 1) .

Answer 1

`(x+2)^2 + (y-1)^2 = 25`

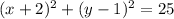
Explanation:

We want to write the equation of a circle with a diameter of 10 units centered on (-2, 1).

Recall that the equation of a circle has the standard form:

`(x-h)^2 + (y-k)^2 = r^2`

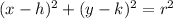
Where (h, k) is the center and r is the radius.

Since our diameter is 10, our radius is 5.

And since the center is at (-2, 1), h = -2 and k = 1.

Substitute:

`\displaystyle (x - (-2))^2 + (y - (1))^2 = (5)^2`

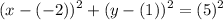
And simplify. Hence, our equation is:

`(x+2)^2 + (y-1)^2 = 25`