Answer:
- reflection over the x-axis
- vertical compression by a factor of 1/3
- vertical translation 3 units down
- reflection over the y-axis (negative coefficient of x)
- horizontal compression by a factor of 1/2
- translation 1 unit to the right (x replaced by x-1)
Explanation:
The various scaling and translation transformations of interest are ...
- g(x) = -f(x) -- reflection over the x-axis
- g(x) = k·f(x) -- vertical scaling by a factor of k (k>1 = expansion)
- g(x) = f(x) +k -- vertical translation by k (k>0 = up)
- g(x) = f(-x) -- reflection over the y-axis
- g(x) = f(x/k) -- horizontal scaling by a factor of k (k>1 = expansion)
- g(x) = f(x -k) -- horizontal translation by k (k>0 = right)
__
In terms of the vertical transformations, we have ...
- reflection over the x-axis (leading minus sign)
- vertical compression by a factor of 1/3
- vertical translation 3 units down (-3 added to the function value)
__
The argument of the function can be written differently to make it easier to see the horizontal transformations.
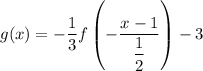
This shows you the horizontal transformations are ...
- reflection over the y-axis (negative coefficient of x)
- horizontal compression by a factor of 1/2
- translation 1 unit to the right (x replaced by x-1)