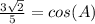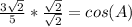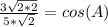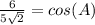One is given the following:
One is asked to prove the following:
In order to prove the statement above, one will need to use a trigonometric identity. In this case, the following identity is the most relevant in the proof.
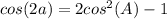
One can manipulate this identity to suit the needs of the given problem:
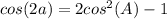
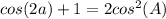
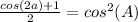
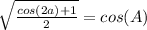
Now substitute the given information into this identity,
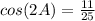
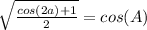
Substitute,
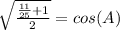
Simplify, remember, any number over itself equals (1) and, in order to add two fractions, they must have the same denominator.
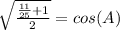
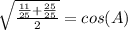
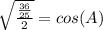
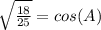
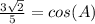
Manipulate so that it resembles the given information; remember, any number over itself is (1), multiplying an equation by (1) doesn't change it,