Answer:
A. 1/3
B. √10
C. -1, 1
D. √8, 6
E. congruent and opposite pairs parallel
F. perpendicular, not congruent
G. rhombus, explanation below
Explanation:
Hey there! I'm happy to help!
-----------------------------------------------------------------
A.
Slope is the rise over the run. Let's look at F to G.
We are going from -1 to 2 on our x-axis (run), so our run is 3 units.
Our rise is 1 unit as we go from 2 to 3 on the y-axis.
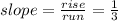
This slope is the same for all of the sides.
-----------------------------------------------------------------
B.
We will use the distance formula (which is basically just the Pythagorean Theorem) to calculate the length of each side. Let's go between F and G again, but this distance is the same for all the sides.
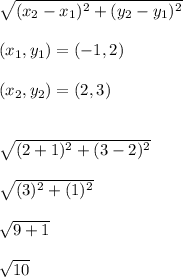
-----------------------------------------------------------------
C.
The diagonals are the lines that connect the non-adjacent vertices.
Our two diagonals are FH and GE.
-----------------------------
FH
We go from x-value -1 to 1 from F to H, so our run is 2.
We go from y-value 2 to 0. so our rise is -2.

-----------------------------
GE
We go from x-value -2 to 2 from E to G, so our run is 4.
We go from y-value -1 to 3. so our rise is 4.
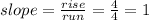
-----------------------------------------------------------------
D.
Let's use the distance formula on each of our diagonals.
-----------------------------
FH
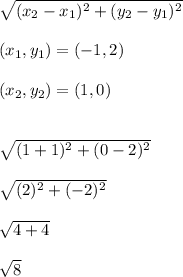
-----------------------------
GE
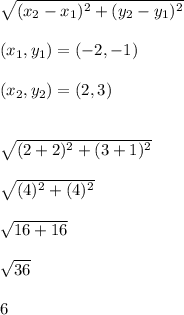
-----------------------------------------------------------------
E.
They are congruent as they all have the same length (√10) and the opposite sides are parallel as they have the same slope (1/3)
-----------------------------------------------------------------
F.
They are perpendicular diagonals as their slopes are negative reciprocals (1 and -1), and they are not congruent as they have different lengths (√8 and 6).
-----------------------------------------------------------------
G.
Parallelogram- quadrilateral with opposite pairs of parallel sides.
Rhombus- a parallelogram with four equal sides
Square- a rhombus with four right angles
We can see that this is a parallelogram as we saw that the opposite sides are parallel due to having the same slope, and the perpendicular diagonals show that as well. This is also a rhombus because if we use that distance formula on all the sides, it will be the same. It is not a square though because it does not have four right angles, so this is a rhombus.
-----------------------------------------------------------------
Have a wonderful day and keep on learning!