Question

How many different 4 card hands can be drawn from a set of 30 cards

Answer 1

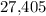`27,\!405` if:

• The cards are drawn without replacement,
• All cards in this set are distinct from one another, and
• The ordering of the four chosen cards does not matter.

Explanation:

`\displaystyle \genfrac{(}{)}{0}{}{30}{4} = (30 * 29 * 28 * 27)/(4 * 3 * 2 * 1) = 27,\!405`.

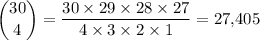Assume for now that the ordering of the four cards does matter. Hands like
`\verb!A!\, \verb!B!\, \verb!C!\, \verb!D!` and
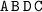`\verb!A!\, \verb!B!\, \verb!D!\, \verb!C!` would then be considered different from one another.

There would
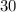`30` choices for the first card. Since the first card was not returned to the pile, there would be only
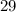`29` choices for the second card. Likewise, there would be
`28` choices for the third card and
`27` for the fourth.

By this reasoning, there would be
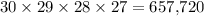`30 * 29 * 28 * 27 = 657,\!720` different ways to draw a hand of four cards from this set when the ordering of these four cards do matter.

However, in many card games, once a hand of cards is drawn, the ordering of cards within that hand does not matter. In other words, hands like
`\verb!A!\, \verb!B!\, \verb!C!\, \verb!D!` and
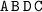`\verb!A!\, \verb!B!\, \verb!D!\, \verb!C!` would not be considered as distinct from one another.

In that case, the
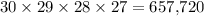`30 * 29 * 28 * 27 = 657,\!720` ways of drawing cards would include a large number of duplicates.

There are be
`4 * 3 * 2 * 1 = 24` ways to arrange a hand of four cards when the order matter. Hence, when the ordering within a hand no longer matters, each hand of four cards would have been counted
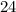`24` times among those
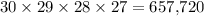`30 * 29 * 28 * 27 = 657,\!720` ways.

Therefore, when the ordering of cards within a set does not matter,
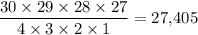`\displaystyle (30 * 29 * 28 * 27)/(4 * 3 * 2 * 1) = 27,\!405` would give the number of distinct ways to draw a hand of four out of this set of thirty distinct cards.