Answer:
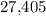 if:
if:
- The cards are drawn without replacement,
- All cards in this set are distinct from one another, and
- The ordering of the four chosen cards does not matter.
Explanation:
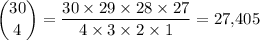 .
.
Assume for now that the ordering of the four cards does matter. Hands like
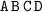 and
and
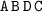 would then be considered different from one another.
would then be considered different from one another.
There would
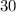 choices for the first card. Since the first card was not returned to the pile, there would be only
choices for the first card. Since the first card was not returned to the pile, there would be only
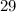 choices for the second card. Likewise, there would be
choices for the second card. Likewise, there would be
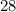 choices for the third card and
choices for the third card and
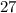 for the fourth.
for the fourth.
By this reasoning, there would be
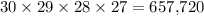 different ways to draw a hand of four cards from this set when the ordering of these four cards do matter.
different ways to draw a hand of four cards from this set when the ordering of these four cards do matter.
However, in many card games, once a hand of cards is drawn, the ordering of cards within that hand does not matter. In other words, hands like
 and
and
 would not be considered as distinct from one another.
would not be considered as distinct from one another.
In that case, the
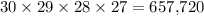 ways of drawing cards would include a large number of duplicates.
ways of drawing cards would include a large number of duplicates.
There are be
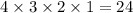 ways to arrange a hand of four cards when the order matter. Hence, when the ordering within a hand no longer matters, each hand of four cards would have been counted
ways to arrange a hand of four cards when the order matter. Hence, when the ordering within a hand no longer matters, each hand of four cards would have been counted
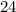 times among those
times among those
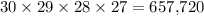 ways.
ways.
Therefore, when the ordering of cards within a set does not matter,
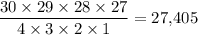 would give the number of distinct ways to draw a hand of four out of this set of thirty distinct cards.
would give the number of distinct ways to draw a hand of four out of this set of thirty distinct cards.