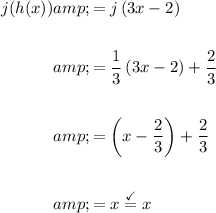Question

Suppose h(x)=3x-2 and j(x) = ax +b. Find a relationship between a and b such that h(j(x)) = j(h(x))

Probably a simple answer, but I'm completely lost at what I'm being asked here.

Answer 1

`\displaystyle a = (1)/(3) \text{ and } b = (2)/(3)`

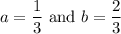
Explanation:

We can use the definition of inverse functions. Recall that if two functions, f and g are inverses, then:

`\displaystyle f(g(x)) = g(f(x)) = x`

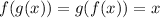
So, we can let j be the inverse function of h.

Function h is given by:

`\displaystyle h(x) = y = 3x-2`

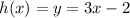
Find its inverse. Flip variables:

`x = 3y - 2`

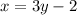
Solve for y. Add:

`\displaystyle x + 2 = 3y`

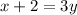
Hence:

`\displaystyle h^(-1)(x) = j(x) = (x+2)/(3) = (1)/(3) x + (2)/(3)`

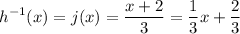
Therefore, a = 1/3 and b = 2/3.

We can verify our solution:

`\displaystyle \begin{aligned} h(j(x)) &= h\left( (1)/(3) x + (2)/(3)\right) \\ \\ &= 3\left((1)/(3)x + (2)/(3)\right) -2 \\ \\ &= (x + 2) -2 \\ \\ &= x \end{aligned}`

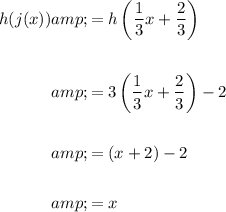
And:

`\displaystyle \begin{aligned} j(h(x)) &= j\left(3x-2\right) \\ \\ &= (1)/(3)\left( 3x-2\right)+(2)/(3) \\ \\ &=\left( x- (2)/(3)\right) + (2)/(3) \\ \\ &= x \stackrel{\checkmark}{=} x\end{aligned}`