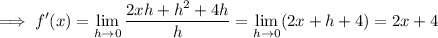Question

Derivatives concept:

Exercises using the definition of derivatives:

(Full development)

Answer 1

(A) f(x) = 7 is constant, so f(x + h) = 7, too, which makes f(x + h) - f(x) = 0. So f'(x) = 0.

(B) f(x) = 5x + 1 ==> f(x + h) = 5 (x + h) + 1 = 5x + 5h + 1

==> f(x + h) - f(x) = 5h

Then

`\displaystyle f'(x) = \lim_(h\to0)\frac{5h}h = \lim_(h\to0)5 = 5`

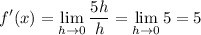
(C) f(x) = x ² + 3 ==> f(x + h) = (x + h)² + 3 = x ² + 2xh + h ² + 3

==> f(x + h) - f(x) = 2xh + h ²

`\implies\displaystyle f'(x) = \lim_(h\to0)\frac{2xh+h^2}h = \lim_(h\to0)(2x+h) = 2x`

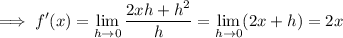
(D) f(x) = x ² + 4x - 1 ==> f(x + h) = (x + h)² + 4 (x + h) - 1 = x ² + 2xh + h ² + 4x + 4h - 1

==> f(x + h) - f(x) = 2xh + h ² + 4h

`\implies \displaystyle f'(x) = \lim_(h\to0)\frac{2xh+h^2+4h}h = \lim_(h\to0)(2x+h+4) = 2x+4`