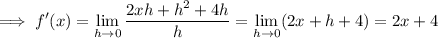(A) f(x) = 7 is constant, so f(x + h) = 7, too, which makes f(x + h) - f(x) = 0. So f'(x) = 0.
(B) f(x) = 5x + 1 ==> f(x + h) = 5 (x + h) + 1 = 5x + 5h + 1
==> f(x + h) - f(x) = 5h
Then
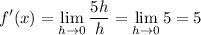
(C) f(x) = x ² + 3 ==> f(x + h) = (x + h)² + 3 = x ² + 2xh + h ² + 3
==> f(x + h) - f(x) = 2xh + h ²
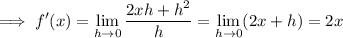
(D) f(x) = x ² + 4x - 1 ==> f(x + h) = (x + h)² + 4 (x + h) - 1 = x ² + 2xh + h ² + 4x + 4h - 1
==> f(x + h) - f(x) = 2xh + h ² + 4h