Answer:
The two substances will have the same volume after approximately 3.453 hours.
Explanation:
The volume of substance A (measured in cubic centimeters) increases at a rate represented by the equation:

Where t is measured in hours.
And substance B is represented by the equation:
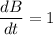
We are also given that at t = 0, A(0) = 3 and B(0) = 5.
And we want to find the time(s) t for which both A and B will have the same volume.
You are correct in that B(t) is indeed t + 5. The trick here is to multiply both sides by dt. This yields:
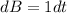
Now, we can take the integral of both sides:
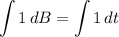
Integrate. Remember the constant of integration!
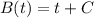
Since B(0) = 5:
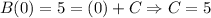
Hence:
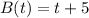
We can apply the same method to substance A. This yields:
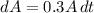
We will have to divide both sides by A:
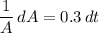
Now, we can take the integral of both sides:
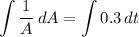
Integrate:
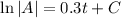
Raise both sides to e:
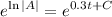
Simplify:
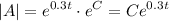
Note that since C is an arbitrary constant, e raised to C will also be an arbitrary constant.
By definition:

Since A(0) = 3:
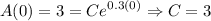
Therefore, the growth model of substance A is:

To find the time(s) for which both substances will have the same volume, we can set the two functions equal to each other:
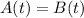
Substitute:
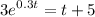
Using a graphing calculator, we can see that the intersect twice: at t ≈ -4.131 and again at t ≈ 3.453.
Since time cannot be negative, we can ignore the first solution.
In conclusion, the two substances will have the same volume after approximately 3.453 hours.