Answer:
The point (11, 5) is NOT on the parabola.
Explanation:
Let
 be any point on the parabola
be any point on the parabola
Let
 be the focus
be the focus
Let
 be the the directrix
be the the directrix
Distance between
 and the focus:
and the focus:
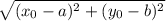
Distance between
 and the directrix is
and the directrix is

Given:
- focus (6, 4)
- directrix y = 0
Therefore:
Distance between
 and the focus:
and the focus:
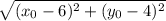
Distance between
 and the directrix is
and the directrix is
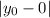
Equate the two expressions and solve for
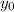 :
:
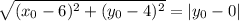
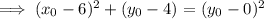
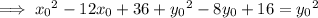
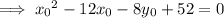
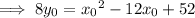
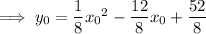
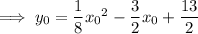
Now rewrite with (x, y):
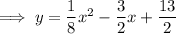
Therefore, this is the equation of the parabola
To determine if the point (11, 5) is on the parabola, input x = 11 into the equation:
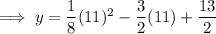
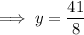
So the point (11, 5) is NOT on the parabola.