Answer: Choice B
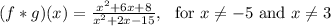
=================================================
Work Shown:
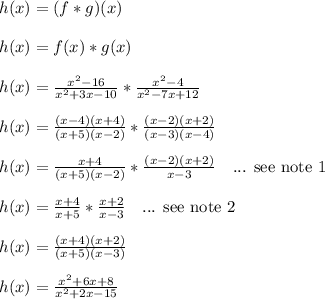
note 1: A pair of (x-4) terms canceled
note 2: A pair of (x-2) terms canceled
------------------------------
Extra info (optional section):
The fact that
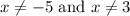 is to avoid a division by zero error in the simplified version of h(x).
is to avoid a division by zero error in the simplified version of h(x).
I would argue that
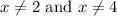 should be thrown in as well simply so that the domains match up perfectly with the original f(x) and g(x) functions.
should be thrown in as well simply so that the domains match up perfectly with the original f(x) and g(x) functions.
So I think the full domain should be that x is any real number but
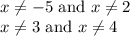
Put another way: if x = 2 is allowed in h(x), then that clashes with the fact that it's not allowed in f(x). The same idea happens with x = 4 but with g(x) this time. It's possible your teacher glossed this fact over, or ran out of room.