Answer:
32π²
Explanation:
To solve this, we can use the washer method.
We can start by dividing the donut into horizontal sections. Each horizontal section is a hollow cylinder, with the inner cylinder's radius being the difference between x=4 and x²+y²=4, which can also be written as x = √(4-y²) (we do not need the negative x values as the inner cylinder does not encompass any part of the circle). This is (4-√(4-y²)) .
Similarly, the outer radius will be equal to the difference between 4 and the other side of the circle. This encompasses the circle and the extra area in between, so x will be negative here, making it (4-(-√(4-y²)) = 4+√(4-y²).
The area of the cylinder for a given Δy can be represented by
(4+√(4-y²))²πΔy - (4-√(4-y²))²πΔy. This space represents a cylinder in the donut created with the height being Δy. Simplifying the equation, we get
(4+√(4-y²))²πΔy - (4-√(4-y²))²πΔy = πΔy((4+√(4-y²))²- (4-√(4-y²))²)
(4+√(4-y²))²- (4-√(4-y²))² = 16+8√(4-y²) + 4-y² - (16-8√(4-y²)+4-y²)
= 16√(4-y²)
(4+√(4-y²))²πΔy - (4-√(4-y²))²πΔy = 16√(4-y²)πΔy
The donut ranges from all y values from -2 to 2, and to add all the areas of the cylinders up between these y values, we can make this an integral,
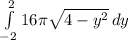
perform u substitution, make y = 2sin(u). If y=2sin(u), then y/2 = sin(u) and arcsin(y/2) = u
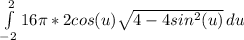
take the 32π out of the integral
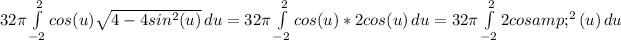
take the 2 out of the integral
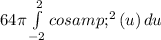
One reduction formula we can use here is that
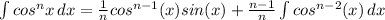
Applying that here, we get
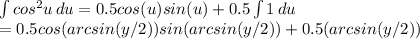
take that cos(arcsin(x)) = √(1-x²) and sin(arcsin(x)) = x and we get
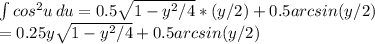
multiply this back with the 64π to get
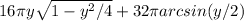
as our integral. Applying this to the bounds of [-2, 2], we get
16π(2)√(1-4/4) + 32πarcsin(1) - (16π(-2)√(1-4/4) + 32πarcsin(-1))
= 0 + 32π(π/2) - 32π(-π/2)
= 16π²+16π²
= 32π²
as our answer