Question

Trigonometric ratios
class 9
please answer my questions​

Answer 1

Explanation:

Hi there!

Please see the answer in the picture.

Hope it helps!

Answer 2

1. Approach

One is given a trigonometric equation with and one is asked to prove that it is true. Using the attached image, combined with the knowledge of trigonometry, one can evaluate each trigonometric function. Then one can simplify each ratio to solve. To yield the most accurate result, one has to each of the ratios in a fractional form, rather than simplifying it into a decimal form. Remember the right angle trigonometric ratios, these ratios describe the relationship between the sides and angles in a right triangle. Such ratios are as follows,

`sin(\theta)=(opposite)/(hypotenuse)\\\\cos(\theta)=(adjacent)/(hypotenuse)\\\\tan(\theta)=(opposite)/(adjacent)\\\\csc(\theta)=(hypotenuse)/(opposite)\\\\sec(\theta)=(hypotenuse)/(adjacent)\\\\cot(\theta)=(adjacent)/(opposite)`

Please note that the terms (opposite) and (adjacent) are relative to the angle uses in the ratio, however the term (hypotenuse) refers to the side opposite the right angle, this side never changes its name. Use these ratios to evaluate the trigonometric functions. Then simplify to prove the identity.

2. Problem (9)

`(sin(60)+cos(30))/(1+sin(30)+cos(60))=sin(60)`

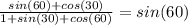
As per the attached image, the following statements regarding the value of each ratio can be made:

`sin(60)=(√(3))/(2)\\\\cos(30)=(√(3))/(2)\\\\sin(30)=(1)/(2)\\\\cos(60)=(1)/(2)`

Substitute,

`(sin(60)+cos(30))/(1+sin(30)+cos(60))=sin(60)`

`((√(3))/(2)+(√(3))/(2))/(1+(1)/(2)+(1)/(2))=(√(3))/(2)`

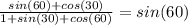
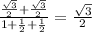
Simplify,

`((√(3))/(2)+(√(3))/(2))/(1+(1)/(2)+(1)/(2))=(√(3))/(2)`

`((2√(3))/(2))/(1+(1)/(2)+(1)/(2))=(√(3))/(2)`

`((2√(3))/(2))/(1+1)=(√(3))/(2)`

`(√(3))/(1+1)=(√(3))/(2)`

`(√(3))/(2)=(√(3))/(2)`

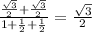
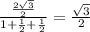
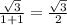
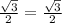
Thus, this equation is true.

2. Problem (10)

Use a similar strategy to evaluate this equation,

`(1-cos(30))/(sin(30))=(1-cot(60))/(1+cot(60))`

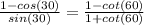
Use the attached image to evaluate the ratios.

`cos(30)=(√(3))/(2)\\\\sin(30)=(1)/(2)\\\\cot(60)=(1)/(√(3))`

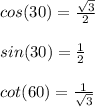
Substitute,

`(1-cos(30))/(sin(30))=(1-cot(60))/(1+cot(60))`

`(1-(√(3))/(2))/((1)/(2))=(1-(1)/(√(3)))/(1+(1)/(√(3)))`

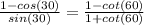
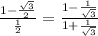
Simplify,

`(1-(√(3))/(2))/((1)/(2))=(1-(1)/(√(3)))/(1+(1)/(√(3)))`

`((2-√(3))/(2))/((1)/(2))=(1-(1)/(√(3)))/(1+(1)/(√(3)))`

`((2-√(3))/(2))/((1)/(2))=((√(3)-1)/(√(3)))/(1+(1)/(√(3)))`

`((2-√(3))/(2))/((1)/(2))=((√(3)-1)/(√(3)))/((√(3)+1)/(√(3)))`

`2-√(3)=((√(3)-1)/(√(3)))/((√(3)+1)/(√(3)))`

`2-√(3)=(√(3)-1)/(√(3))*(√(3))/(√(3)+1)}`

`2-√(3)=(√(3)-1)/(√(3)+1)`

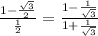
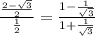
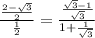
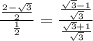
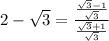
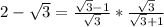
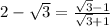
Rationalize the denominator,

`2-√(3)=(√(3)-1)/(√(3)+1)`

`2-√(3)=(√(3)-1)/(√(3)+1)*(√(3)-1)/(√(3)-1)`

`2-√(3)=((√(3)-1)^2)/(3-1)`

`2-√(3)=(3-2√(3)+1)/(2)`

`2-√(3)=(4-2√(3))/(2)`

`2-√(3)=2-√(3)`

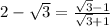
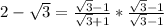
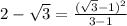
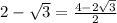
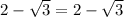
Therefore, this equation is also true.