Question

A number is equal to twice a smaller number plus 3. The same number is equal to twice the sum of the smaller number and 1. How many solutions are possible for this situation?

* Infinitely many solutions exist because the two situations describe the same line.
* Exactly one solution exists because the situation describes two lines that have different slopes and different y-intercepts.
* No solutions exist because the situation describes two lines that have the same slope and different y-intercepts.
* Exactly one solution exists because the situation describes two lines with different slopes and the same y-intercept.

Answer 1

There is no solution to this.

Explanation :

We have a double system of equation to solve. Let x be the big number and let y be the smaller number, such that y < x.

x is equal to twice a smaller number plus 3, which translates into : x = 2y + 3

and x is equal to twice the sum of the smaller number and 1 : x = 2 * (y + 1)

We get this system to solve :
`\left \{{{x=2y+3} \atop {x=2(y+1)}} \right. \left \{{{x-2y=3} \atop {x-2y=2}} \right.`

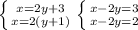
It's either x minus 2y equals 3, or x minus 2y = 2 but it can't be both. No solutions exist because the situation describes two lines that have the same slope and different y-intercepts