Answer:
x = 0 and 3 other real roots. See below.
Explanation:
This is what you wrote:
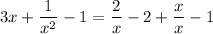
I don't think that is what you meant to write.
I think you meant to write this:
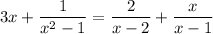
I'm going to answer the second equation because that is what I think you meant.

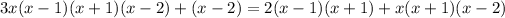
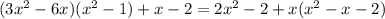
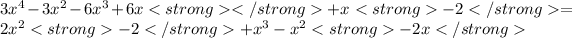
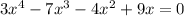

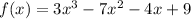

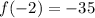
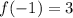
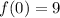
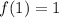
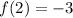
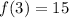
One root is x = 0.
There is a root between x = -2 and x = -1.
There is a root between x = 1 and x = 2.
There is a root between x = 2 and x = 3.
Plot the graph of f(x) = 3x^3 - 7x^2 - 4x + 9 and try to read the other three roots.