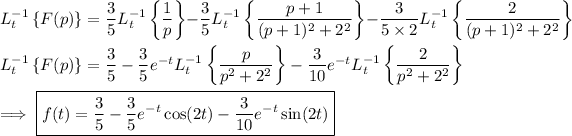It looks like we're given the Laplace transform of f(t),
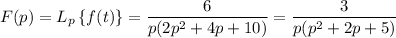
Start by splitting up F(p) into partial fractions:
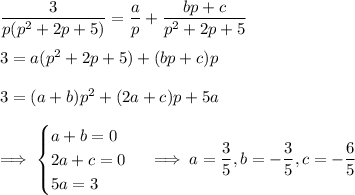
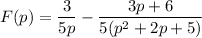
Complete the square in the denominator,
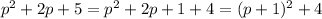
and rewrite the numerator in terms of p + 1,
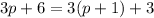
Then splitting up the second term gives
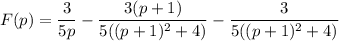
Now take the inverse transform: