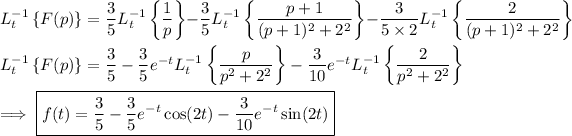Question

Hãy tìm hàm gốc f(t) có hàm ảnh Laplace như dưới đây:
F(p)=6/p(2p^2+4p +10)

Answer 1

It looks like we're given the Laplace transform of f(t),

`F(p) = L_p\left\{f(t)\right\} = \frac6{p(2p^2+4p+10)} = \frac3{p(p^2+2p+5)}`

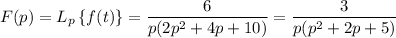
Start by splitting up F(p) into partial fractions:

`\frac3{p(p^2+2p+5)} = \frac ap + (bp+c)/(p^2+2p+5) \\\\ 3 = a(p^2+2p+5) + (bp+c)p \\\\ 3 = (a+b)p^2 + (2a+c)p + 5a \\\\ \implies \begin{cases}a+b=0 \\ 2a+c=0 \\ 5a=3\end{cases} \implies a=\frac35,b=-\frac35, c=-\frac65`

`F(p) = \frac3{5p} - (3p+6)/(5(p^2+2p+5))`

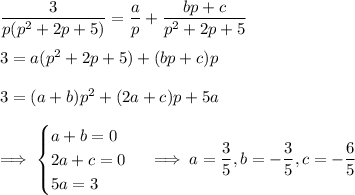
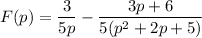
Complete the square in the denominator,

`p^2+2p+5 = p^2+2p+1+4 = (p+1)^2+4`

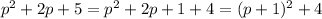
and rewrite the numerator in terms of p + 1,

`3p+6 = 3(p+1) + 3`

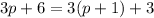
Then splitting up the second term gives

`F(p) = \frac3{5p} - (3(p+1))/(5((p+1)^2+4)) - \frac3{5((p+1)^2+4)}`

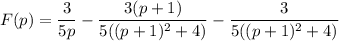
Now take the inverse transform:

`L^(-1)_t\left\{F(p)\right\} = \frac35 L^(-1)_t\left\{\frac1p\right\} - \frac35 L^(-1)_t\left\{(p+1)/((p+1)^2+2^2)\right\} - \frac3{5*2} L^(-1)_t\left\{\frac2{(p+1)^2+2^2}\right\} \\\\ L^(-1)_t\left\{F(p)\right\} = \frac35 - \frac35 e^(-t) L^(-1)_t\left\{\frac p{p^2+2^2}\right\} - \frac3{10} e^(-t) L^(-1)_t\left\{\frac2{p^2+2^2}\right\} \\\\ \implies \boxed{f(t) = \frac35 - \frac35 e^(-t) \cos(2t) - \frac3{10} e^(-t) \sin(2t)}`