Step-by-step explanation:
Let
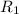 and
and
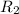 be the the resistances of the resistors. We are given that
be the the resistances of the resistors. We are given that
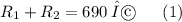
and
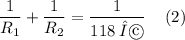
From Eqn(1), we can write
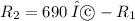
and then plug this into Eqn(2):
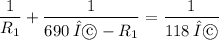
or
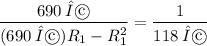
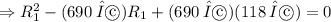
or
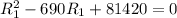
Using the quadratic formula, we find that the above equation has two roots:

This means that if you choose one root value for
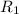 , the other root will be the value for
, the other root will be the value for
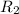 .
.