You're looking for a solution of the form

Differentiating twice yields
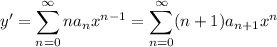

Substitute these series into the DE:
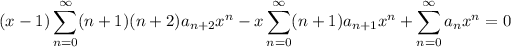
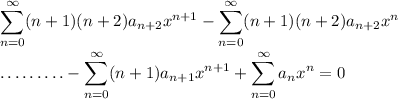
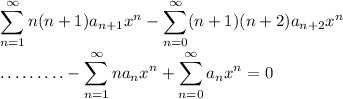
Two of these series start with a linear term, while the other two start with a constant. Remove the constant terms of the latter two series, then condense the remaining series into one:
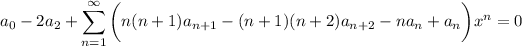
which indicates that the coefficients in the series solution are governed by the recurrence,
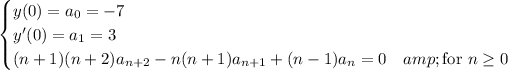
Use the recurrence to get the first few coefficients:
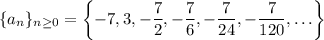
You might recognize that each coefficient in the n-th position of the list (starting at n = 0) involving a factor of -7 has a denominator resembling a factorial. Indeed,
-7 = -7/0!
-7/2 = -7/2!
-7/6 = -7/3!
and so on, with only the coefficient in the n = 1 position being the odd one out. So we have
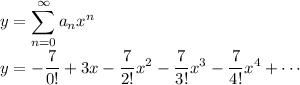
which looks a lot like the power series expansion for -7eˣ.
Fortunately, we can rewrite the linear term as
3x = 10x - 7x = 10x - 7/1! x
and in doing so, we can condense this solution to
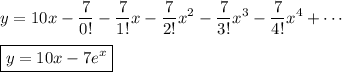
Just to confirm this solution is valid: we have
y = 10x - 7eˣ ==> y (0) = 0 - 7 = -7
y' = 10 - 7eˣ ==> y' (0) = 10 - 7 = 3
y'' = -7eˣ
and substituting into the DE gives
-7eˣ (x - 1) - x (10 - 7eˣ ) + (10x - 7eˣ ) = 0
as required.