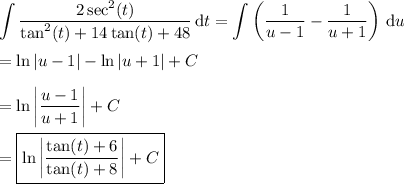Complete the square in the denominator to get
tan²(t ) + 14 tan(t ) + 48 = tan²(t ) + 14 tan(t ) + 49 - 1
… = (tan(t ) + 7)² - 1
Substitute u = tan(t ) + 7 and du = sec²(t ) dt. Then the integral becomes
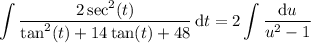
Separate the integrand into partial fractions:
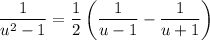
Then we get