Answer: C. a set of input values
The domain is the set of allowed x values, aka input values.
With fairly many domain problems, one thing to look out for are things like potential division by zero issues. For example, if you had the function f(x) = 2/(x-3), then we want to avoid the denominator x-3 from being zero. Because x = 3 makes x-3 equal to zero, this means we must kick x = 3 out of the domain; however, any other real number will work. This example function therefore has the domain of any real number but 3.
Square roots are another thing that often comes up with domain problems. One example could be g(x) = sqrt(x+5). We'd want the x+5 to never be negative. Solving
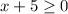 leads to
leads to
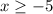 to tell us what set of input x values we can plug in: namely anything -5 or larger.
to tell us what set of input x values we can plug in: namely anything -5 or larger.
Other types of domain problems can occur, but those two types are most common in my experience.