Answer:
Explanation:
The slope describes the direction and steepness of a line. The formula is:
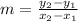
Where (x₁, y₁) and (x₂, y₂) are the points the line contains. For this problem, the line contains the points (2,7) and (-5, -4). Therefore:
- x₁= 2
- y₁ = 7
- x₂ = -5
- y₂ = -4
Substitute these values into the formula.
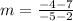
Solve the numerator (-4 -7 = -11).
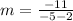
Solve the denominator (-5-2 = -7).
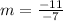
Simplify the fraction. The 2 negative signs cancel each other out.
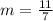
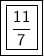
The slope of the line is 11/7