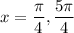Question

Find all the solutions of the equation in the interval [0, 2pi)

sin2x-1=0

show work pls

Answer 1

`\displaystyle x = (\pi)/(4) , (5\pi)/(4)`

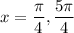
Explanation:

We want to find all solutions to the equation:

`\displaystyle \sin 2x - 1 = 0`

In the interval [0, 2π).

First, add one to both sides:

`\displaystyle \sin 2x = 1`

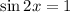
Recall that sin(u) equals one whenever u = π/2. This will occur for every rotation. Hence, we can say that u = π/2 + 2nπ where n is an integer.

And in this case, u = 2x. Thus:

`\displaystyle 2x = (\pi)/(2) + 2n\pi\text{ where } n\in\mathbb{Z}`

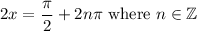
Dividing both sides by two yields:

`\displaystyle x = (\pi)/(4) + n\pi \text{ where } n\in \mathbb{Z}`

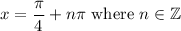
There are two values of x in the interval [0, 2π) given when n = 0 and n = 1:

`\displaystyle x _ 1= (\pi)/(4) \text{ and } x_2 = (\pi)/(4) + (1)\pi = (5\pi)/(4)`

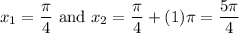
Any other solutions will be outside our interval.

Therefore, our solutions are:

`\displaystyle x = (\pi)/(4) , (5\pi)/(4)`