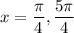Answer:
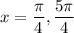
Explanation:
We want to find all solutions to the equation:
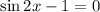
In the interval [0, 2π).
First, add one to both sides:
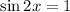
Recall that sin(u) equals one whenever u = π/2. This will occur for every rotation. Hence, we can say that u = π/2 + 2nπ where n is an integer.
And in this case, u = 2x. Thus:
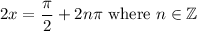
Dividing both sides by two yields:
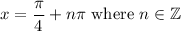
There are two values of x in the interval [0, 2π) given when n = 0 and n = 1:
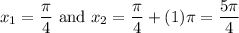
Any other solutions will be outside our interval.
Therefore, our solutions are: