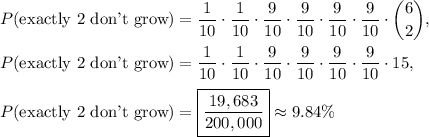Answer:
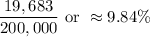
Explanation:
For each planted seed, there is a 90% chance that it grows into a healthy plant, which means that there is a
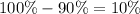 chance it does not grow into a healthy plant.
chance it does not grow into a healthy plant.
Since we are planting 6 seeds, we want to choose 2 that do not grow and 4 that do grow:
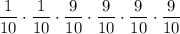
However, this is only one case that meets the conditions. We can choose any 2 out of the 6 seeds to be the ones that don't grow into a healthy plant, not just the first and second ones. Therefore, we need to multiply this by number of ways we can choose 2 things from 6 (6 choose 2):
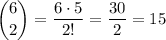
Therefore, we have: