Answer:
The depth of the resulting stream is 3.8 meters.
Step-by-step explanation:
Under the assumption that streams are formed by incompressible fluids, so that volume flow can observed conservation:
 (1)
(1)
All volume flows are measured in cubic meters per second.
Dimensionally speaking, we can determine the depth of the resulting stream (
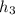 ), in meters, by expanding (1) in this manner:
), in meters, by expanding (1) in this manner:
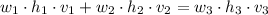
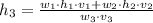 (2)
(2)
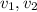 - Speed of the merging streams, in meters per second.
- Speed of the merging streams, in meters per second.
 - Depth of the merging streams, in meters.
- Depth of the merging streams, in meters.
 - Width of the merging streams, in meters.
- Width of the merging streams, in meters.
 - Width of the resulting stream, in meters.
- Width of the resulting stream, in meters.
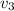 - Speed of the resulting stream, in meters per second.
- Speed of the resulting stream, in meters per second.
If we know that
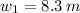 ,
,
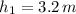 ,
,
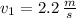 ,
,
 ,
,
 ,
,
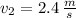 ,
,
 and
and
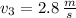 , then the depth of the resulting stream is:
, then the depth of the resulting stream is:
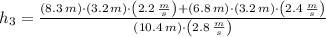
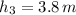
The depth of the resulting stream is 3.8 meters.