Question

C=1/21.22.23+1/22.23.24+................+1/200.201.202

. = là dấu nhân

Answer 1

It looks like you have to find the value of the sum,

`C = \displaystyle \frac1{21*22*23} + \frac1{22*23*24} + \cdots + \frac1{200*201*202}`

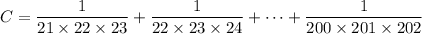
so that the n-th term in the sum is

`\frac1{(21+(n-1))*(21+n)*(21+(n+1))} = \frac1{(n+20)(n+21)(n+22)}`

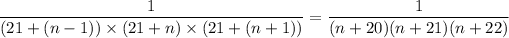
for 1 ≤ n ≤ 180.

We can then write the sum as

`\displaystyle C = \sum_(n=1)^(180) \frac1{(n+20)(n+21)(n+22)}`

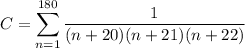
Break up the summand into partial fractions:

`\frac1{(n+20)(n+21)(n+22)} = \frac a{n+20} + \frac b{n+21} + \frac c{n+22}`

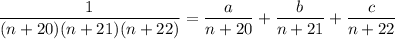
Combine the fractions into one with a common denominator and set the numerators equal to one another:

`1 = a(n+21)(n+22) + b(n+20)(n+22) + c(n+20)(n+21)`

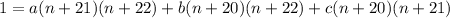
Expand the right side and collect terms with the same power of n :

`1 = a(n^2+43n+462)+b(n^2+42n+440) + c(n^2+41n + 420) \\\\ 1 = (a+b+c)n^2 + (43a+42b+41c)n + 462a+440b+420c`

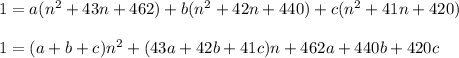
Then

a + b + c = 0

43a + 42b + 41c = 0

462a + 440b + 420c = 1

==> a = 1/2, b = -1, c = 1/2

Now our sum is

`\displaystyle C = \sum_(n=1)^(180) \left(\frac1{2(n+20)}-\frac1{n+21}+\frac1{2(n+22)}\right)`

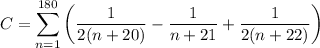
which is a telescoping sum. If we write out the first and last few terms, we have

C = 1/(2×21) - 1/22 + 1/(2×23)

… … + 1/(2×22) - 1/23 + 1/(2×24)

… … + 1/(2×23) - 1/24 + 1/(2×25)

… … + 1/(2×24) - 1/25 + 1/(2×26)

… … + … - … + …

… … + 1/(2×198) - 1/199 + 1/(2×200)

… … + 1/(2×199) - 1/200 + 1/(2×201)

… … + 1/(2×200) - 1/201 + 1/(2×202)

Notice the diagonal pattern of underlined and bolded terms that add up to zero (e.g. 1/(2×23) - 1/23 + 1/(2×23) = 1/23 - 1/23 = 0). So, like a telescope, the sum collapses down to a simple sum of just six terms,

C = 1/(2×21) - 1/22 + 1/(2×22) + 1/(2×201) - 1/201 + 1/(2×202)

which we simplify further to

C = 1/42 - 1/44 - 1/402 + 1/404

C = 1,115/1,042,118 ≈ 0.00106994