It looks like you have to find the value of the sum,
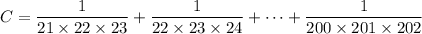
so that the n-th term in the sum is
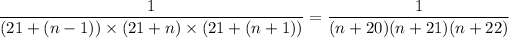
for 1 ≤ n ≤ 180.
We can then write the sum as
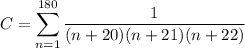
Break up the summand into partial fractions:
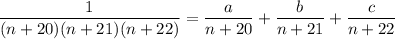
Combine the fractions into one with a common denominator and set the numerators equal to one another:
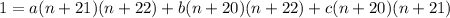
Expand the right side and collect terms with the same power of n :
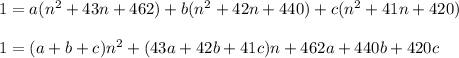
Then
a + b + c = 0
43a + 42b + 41c = 0
462a + 440b + 420c = 1
==> a = 1/2, b = -1, c = 1/2
Now our sum is
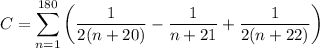
which is a telescoping sum. If we write out the first and last few terms, we have
C = 1/(2×21) - 1/22 + 1/(2×23)
… … + 1/(2×22) - 1/23 + 1/(2×24)
… … + 1/(2×23) - 1/24 + 1/(2×25)
… … + 1/(2×24) - 1/25 + 1/(2×26)
… … + … - … + …
… … + 1/(2×198) - 1/199 + 1/(2×200)
… … + 1/(2×199) - 1/200 + 1/(2×201)
… … + 1/(2×200) - 1/201 + 1/(2×202)
Notice the diagonal pattern of underlined and bolded terms that add up to zero (e.g. 1/(2×23) - 1/23 + 1/(2×23) = 1/23 - 1/23 = 0). So, like a telescope, the sum collapses down to a simple sum of just six terms,
C = 1/(2×21) - 1/22 + 1/(2×22) + 1/(2×201) - 1/201 + 1/(2×202)
which we simplify further to
C = 1/42 - 1/44 - 1/402 + 1/404
C = 1,115/1,042,118 ≈ 0.00106994