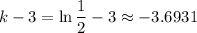Answer:
A)
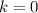
B)
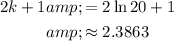
C)
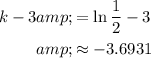
Explanation:
We are given the function:
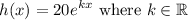
A)
Given that h(1) = 20, we want to find k.
h(1) = 20 means that h(x) = 20 when x = 1. Substitute:
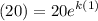
Simplify:
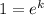
Anything raised to zero (except for zero) is one. Therefore:
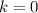
B)
Given that h(1) = 40, we want to find 2k + 1.
Likewise, this means that h(x) = 40 when x = 1. Substitute:
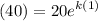
Simplify:
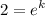
We can take the natural log of both sides:

By definition, ln(e) = 1. Hence:
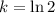
Therefore:
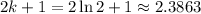
C)
Given that h(1) = 10, we want to find k - 3.
Again, this meas that h(x) = 10 when x = 1. Substitute:
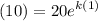
Simplfy:
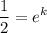
Take the natural log of both sides:
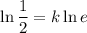
Therefore:
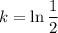
Therefore: