Question

Use the integral test to determine whether the series is convergent or divergent. [infinity] n = 2 n2 n3 + 1 Evaluate the following integral. [infinity] 2 x2 x3 + 1 dx

Answer 1

I think the given series is

`\displaystyle\sum_(n=2)^\infty (n^2)/(n^3+1)`

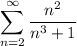
You can use the integral test because the summand is clearly positive and decreasing. Then

`\displaystyle\sum_(n=2)^\infty(n^2)/(n^3+1) > \int_2^\infty(x^2)/(x^3+1)\,\mathrm dx`

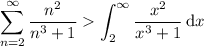
Substitute u = x ³ + 1 and du = 3x ² dx, so the integral becomes

`\displaystyle \int_2^\infty(x^2)/(x^3+1)\,\mathrm dx = \frac13\int_9^\infty\frac{\mathrm du}u = \frac13\ln(u)\bigg|_(u=9)^(u\to\infty)`

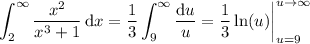
As u approaches infinity, we have ln(u) also approaching infinity (whereas 1/3 ln(9) is finite), so the integral and hence the sum diverges.