Question

Find the remainder when f(x)=x3−4x2−6x−3 f ( x ) = x 3 − 4 x 2 − 6 x − 3 is divided by x+1

Answer 1

The remainder is -2.

Explanation:

According to the Polynomial Remainder Theorem, if we divide a polynomial P(x) by a binomial (x - a), then the remainder of the operation will be given by P(a).

Our polynomial is:

`P(x) = x^3-4x^2-6x-3`

And we want to find the remainder when it's divided by the binomial:

`x+1`

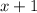
We can rewrite our divisor as (x - (-1)). Hence, a = -1.

Then by the PRT, the remainder will be:

`\displaystyle\begin{aligned} R &= P(-1)\\ &=(-1)^3-4(-1)^2-6(-1)-3 \\ &= (-1)-4(1)+(6)-3 \\ &= -2 \end{aligned}`

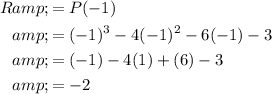
The remainder is -2.