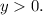Final Answer:
The expression equivalent to
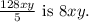
Step-by-step explanation:
To simplify the given expression,
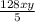 , we divide both the numerator and the denominator by their greatest common factor, which is 5. This simplification yields
, we divide both the numerator and the denominator by their greatest common factor, which is 5. This simplification yields
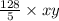 . Further simplifying
. Further simplifying
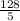 results in 8, giving us the equivalent expression
results in 8, giving us the equivalent expression
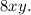
Breaking down the steps, we start with
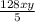 . Dividing both 128 and 5 by 5 simplifies the fraction to
. Dividing both 128 and 5 by 5 simplifies the fraction to
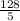 . When multiplied by
. When multiplied by
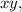 we obtain the simplified expression
we obtain the simplified expression
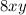 . Therefore,
. Therefore,
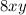 is the equivalent expression to
is the equivalent expression to
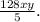
In summary, the process involves dividing by the greatest common factor to simplify the fraction and arrive at the equivalent expression
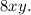
Complete the question:
Which expression is equivalent to
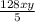 ? Assume
? Assume
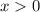 and
and