Question

The base of an aluminum block, which is fixed in place, measures 90 cm by 90 cm, and the height of the block is 60 cm. A force, applied to the upper face and parallel to it, produces a shear strain of 0.0060. The shear modulus of aluminum is . What is the displacement of the upper face in the direction of the applied force

Answer 1

The question is incomplete. The complete question is :

The base of an aluminum block, which is fixed in place, measures 90 cm by 90 cm, and the height of the block is 60 cm. A force, applied to the upper face and parallel to it, produces a shear strain of 0.0060. The shear modulus of aluminum is
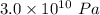`3.0 * 10^(10) \ Pa` . What is the displacement of the upper face in the direction of the applied force?

Solution :

The relation between shear modulus, shear stress and strain,

`$\text{Shear modulus, S =} \frac{\text{Shear stress}}{\text{shear strain}}$`

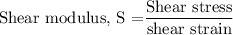
Shear stress = shear modulus (S) x shear strain

`$=3 * 10^(10) * 0.0060$`

`$=1.80 * 10^8$` Pa

`$=180 * 10^6$` Pa

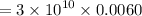
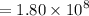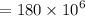`$=180 \ MPa$`

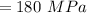
The length represents the distance between the fixed in place portion and where the force is being applied.

Therefore,

`$\text{Displacement} = \text{shear strain} * \text{length}$`

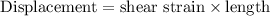
= 0.006 x 60 cm

= 0.360 cm

= 3.6 mm

Thus, the displacement of the upper face is 3.6 mm in the direction of the applied force.