Question

Help me out with these 2 questions for 15 points.

Answer 1

Explanation:

The time dilation formula is given by

`F(t) = (t)/(√(1-v^2))`

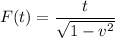
where t is the time measured by the moving observer and F(t) is the time measured by the stationary earth-bound observer and v is the velocity of the moving observer expressed as a fraction of the speed of light.

a) If the observer is moving at 80% of the speed of light and observes an event that lasts for 1 second, a stationary observer will see the same event occurring over a time period of

`F(t) = \frac{1\:\text{s}}{√(1-(0.8)^2)}`

`\:\:\:\:\:\:\:=\frac{1\:\text{s}}{√(1-(0.8)^2)} =\frac{1\:\text{s}}{√(1-(0.64))}`

`\:\:\:\:\:\:\:=1.67\:\text{s}`

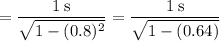
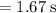
This means that any event observed by this moving observer will be seen by a stationary observer to occur 67% longer.

b) Given:

t = 1 second

F(t) = 2 seconds

We need to find the speed of the observer such that an event seen by this observer will occur twice as long as seen by a stationary observer. Move the term containing the radical to the left side so the equation becomes

`√(1-v^2) = (t)/(F(t))`

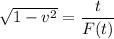
Take the square of both sides, we get

`1 - v^2 =(t^2)/(F^2(t))`

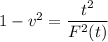
Solving for v, we get

`v^2 = 1 - (t^2)/(F^2(t))`

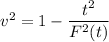
or

`v = \sqrt{1 - (t^2)/(F^2(t))}`

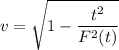
Putting in the values for t and F(t) we get

`v = \sqrt{1 - \frac{(1\:\text{s})^2}{(2\:\text{s})^2}}`

`v = \sqrt{1 - (1)/(4)} = √(0.75)`

`\:\:\:\:=0.866`

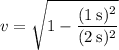
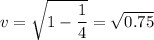
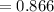
This means that the observer must moves at 86.6% of the speed of light.